If you’ve ever played Sea of Thieves, the game I’m working on as an engineer at Rare Ltd, you may have run afoul of skeletons firing cannons at you while you sail past an island, minding your own business. One of the first pieces of work I did here at Rare was programming the algorithm the skellies use to aim the cannon and provide a sense of emergent danger for players. In this article I’ll give you a peek behind the curtain at how we’d build up the moving parts of a gameplay feature. We’ll go step by step through how I designed the first version of this cannon aiming algorithm, which was released around E3 2017 to our Technical Alpha players. The code may have changed quite a bit in the year since we released it, so it may not exactly match the behaviour you can see in game now.

The brief
First, imagine that we already have the skeleton spawning in response to a ship sailing within range of its cannon, and firing a cannonball every few seconds or so. What the algorithm we’re going to build will do is make it aim the cannon so that each cannonball has a certain chance of hitting, which a designer can configure. A hit must land at some seemingly random point on the ship, whereas a miss must land short of the ship, causing a dramatic splash where the player is most likely to be looking (towards the skeleton).
As well as having to come up with an algorithm that will give players that experience, we have to make our solutions fit into the structure of the code that is already there. The interesting thing in this situation is that due to various quirks of the Unreal behaviour tree system, the code that aims the cannon barrel and the code that fires the cannonballs is completely separate! Like anything in code, it’s possible to make the two systems talk to each other, but whether it’s neat, pragmatic, and time efficient enough to do so is another matter entirely. The aiming code won’t know when the cannonball is going to be fired, so our part of the task is making the skeleton aim the cannon continuously in such a way that the cannonballs can be fired whenever and still give the experience outlined above.
It’s best to develop this kind of algorithm in steps, going from the simplest implementation we can and adding layers of complexity one by one. This way we can make sure each layer works individually, and we can stop when the feature works well as a whole- so we won’t end up working on any tiny polishes players won’t notice.
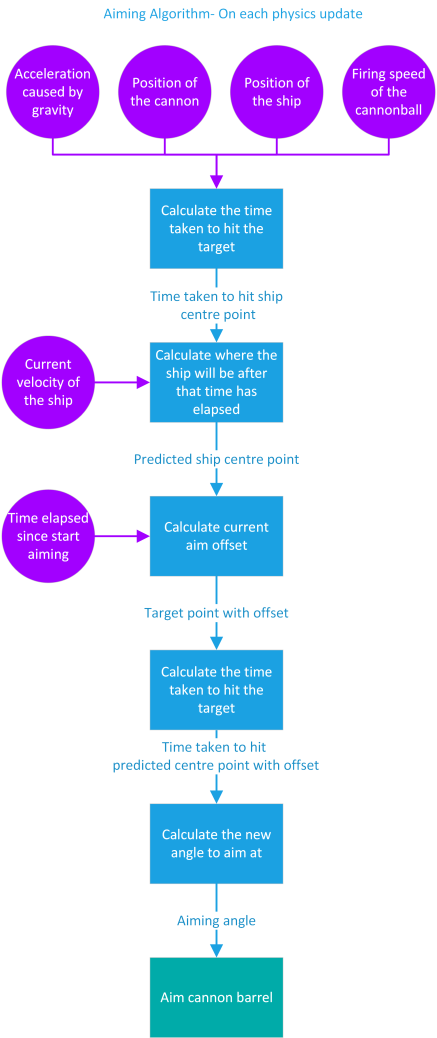
Our first version of the algorithm works so that the skeleton is always aiming directly at the centre of the target ship so that whenever the cannonball is fired it’ll land exactly there. For this we have to calculate what pitch and yaw the cannon needs to be aimed at to hit a given point.
Hitting a fixed point
These equations may bring you vividly back to studying physics in school (sorry for that). They’re sometimes known as the “SUVAT equations” and they link together the properties of any solid object that’s moving under a constant acceleration over any given period of time:
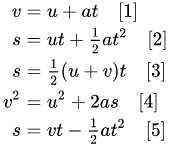
S is the displacement– The difference between the start and end positions.
U is the initial velocity– The speed and direction at the start of the time period we’re calculating.
V is the final velocity– The speed and direction at the end of the time period we’re calculating.
A is the acceleration– The constant acceleration the object is moving under
T is the period of time– This doesn’t have to the whole time period an object is in the air, if we pick any period of time that an object is under constant acceleration these equations will still apply.
To understand how this can represent a cannonball or any other projectile, you might have to think about speed, velocity and acceleration a little differently. It might seem like a cannonball isn’t accelerating at all, because it isn’t speeding up or slowing down while in the air (other than being slowed a little by air resistance, which we can ignore). But while speed is how much distance something travels over a period of time, the velocity is how much the position changes in a period of time, giving it a direction as well as magnitude. Acceleration in this context is how much the velocity changes in the same period of time, not the speed. Because the direction of our cannonball changes during the flight, it’s under acceleration, caused by a force you may know as: gravity! The cannonball is always being pulled downwards by gravity, and each second it will have moved downwards a little more than the last second, while its horizontal position will change by the same amount.

On earth, gravity is essentially always the same, and so we can assume the acceleration caused by it is constant. This is why if you simultaneously drop two objects with very different weights from the same height, they’ll take about the same time to hit the floor (NB: This is providing air resistance acts the same on both of them, which is why a feather falls more slowly than a hammer on earth, but not on the moon). Because we simulate real world physics in the Sea of Thieves world, and because the only acceleration acting on our cannonballs is the constant acceleration caused by gravity, we can use these equations to model the behaviour.
The value we’re trying to calculate is the initial velocity (U), which we have the magnitude of (the cannonball firing speed chosen by the designers) but not the direction (the angle of fire). Using these equations, if we have 3 of the SUVAT values, we can calculate the fourth and fifth. We know the difference between the position we want the cannonball to land and position the cannon is at, which is the displacement (S). We know the constant acceleration caused by gravity (A). We’re one value short. Thankfully, we can use the starting speed of the cannonball, and several facts we know about projectile flight to work out the time of flight (T) using a little mathematical magic. Now we have these values, we can use this equation:
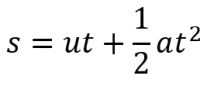
Which we can rearrange like this to give us the U value:
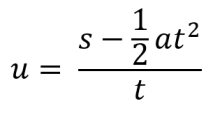
Now we can turn these equations into a set of instructions that the computer can use to take the position of the cannon, the position of the target- and facts like gravity and the firing speed of a cannonball- and give us an angle at which the cannon has to be aimed to hit that point. Here’s how the first version of the algorithm looks:
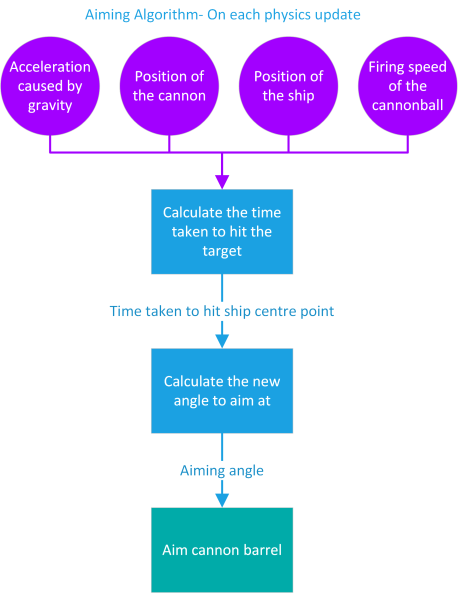
Hitting a moving target
Unfortunately for us, ships move. Cannonballs can take up to 12 seconds or so to reach their target. If we have our skelly aim at where the ship is right now, they may not still be there in 12 seconds’ time. Very unfortunately for us ships turn and speed up and slow down so their speed changes too. However, fortunately for us, their speed doesn’t change very much. We can still create peril for players by approximating where the ship will be by the time the cannonball finishes its flight, on the assumption it will keep travelling at the speed it is now.
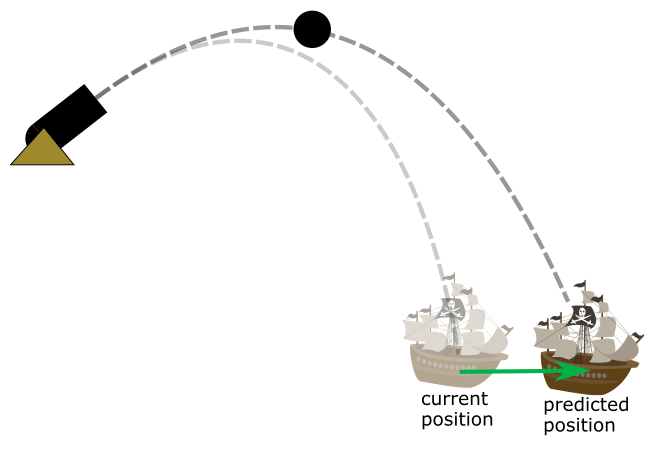
We have a bit of a chicken/egg situation here: we need the cannonball’s flight time to find where the ship will be by the time it hits, but we need this position to find the cannonball’s flight time. We can get around this by performing part of our SUVAT calculations to figure out how long it would take us to hit the ship where it currently is. Usually the ship is travelling sufficiently slowly that using the flight time to the current position instead of the predicted position won’t throw out our calculations by any significant amount. If we assume that the ship will keep travelling at the speed it is now, we use that speed to calculate where it will be after that period of time, and that position will be our new target. We’ll then feed that predicted centre point back into our calculation logic to get an updated angle to aim at:
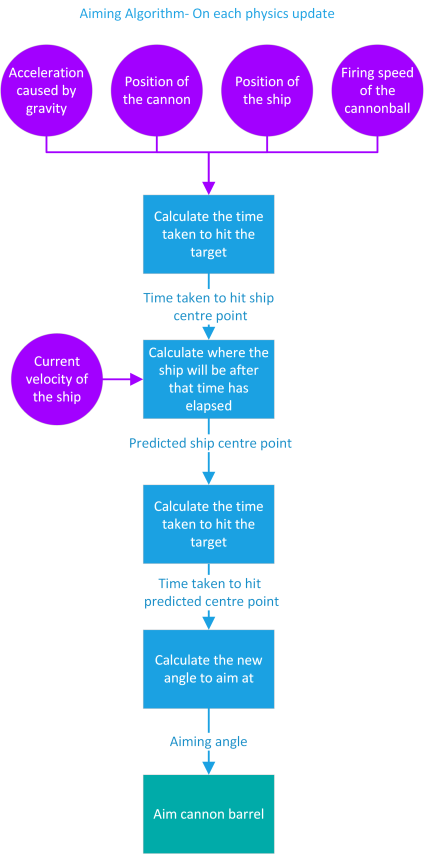
Making it feel real
We all play video games for the raw, authentic experiences, so of course having these reanimated skeletons hit your pirate ship in the exact same spot every time would shatter the realistic illusion of being under attack by a squad of sneaky skellies. There has to be a variation in where they hit. The most obvious solution is to aim at a new random point on the ship each time the skeletons aim, but as we mentioned before, we don’t know when the cannonball is going to be fired so we can’t move the cannon barrel into position ahead of when we shoot.
We want to move our target position all over the ship in a smooth motion, so that the skeletons don’t look like they’re snapping the cannon barrel awkwardly into position. My solution is wobbly aiming by a mathematical function in polar coordinates. What you’ll be familiar with are the functions in “cartesian” coordinates used on most graphs, which take an input of a horizontal x position and output a vertical y position. Polar functions take an input of the angle around a centre point and output a radius, so they’re better for producing circular or spiral shapes.
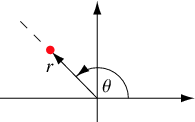
Taking the centre of our target ship as a centre point, we can start with a function that just aims round and round at a constant angular speed, which means the angle of the point we’re aiming at round the centre changes by the same amount every update. If the radius (the distance between the point we’re aiming at and the centre point of the ship) is constant, our mathematical function will look like this and we’ll just be moving the cannon barrel around in circles:
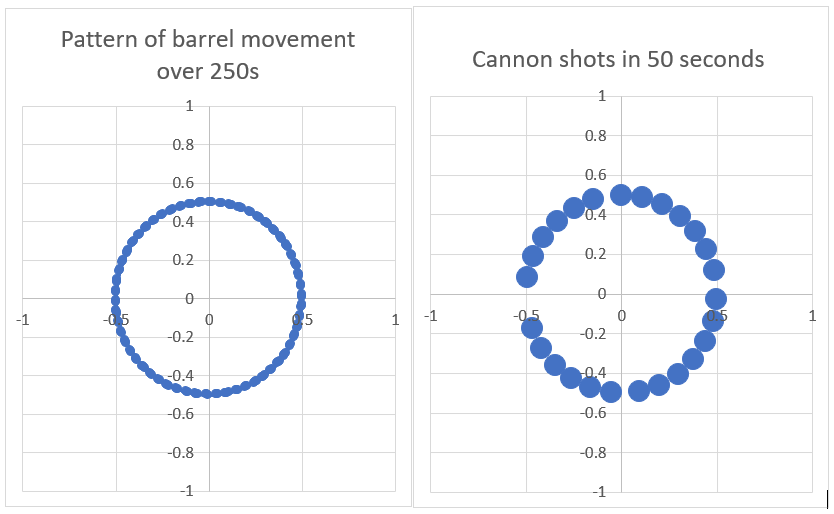
We can now alter this function to vary the radius over time so that the skeleton is aiming in smooth, wobbly circles, and when they’re firing every few seconds we’ll get a seemingly randomly distributed smattering of cannonball hits:

So now we can input the time elapsed since we started the aiming algorithm and our predicted ship centre point into a new step in the algorithm. The new step will calculate what point on the ship we need to be aiming at on each update to produce this “wobbly aiming” effect:
Missing the mark
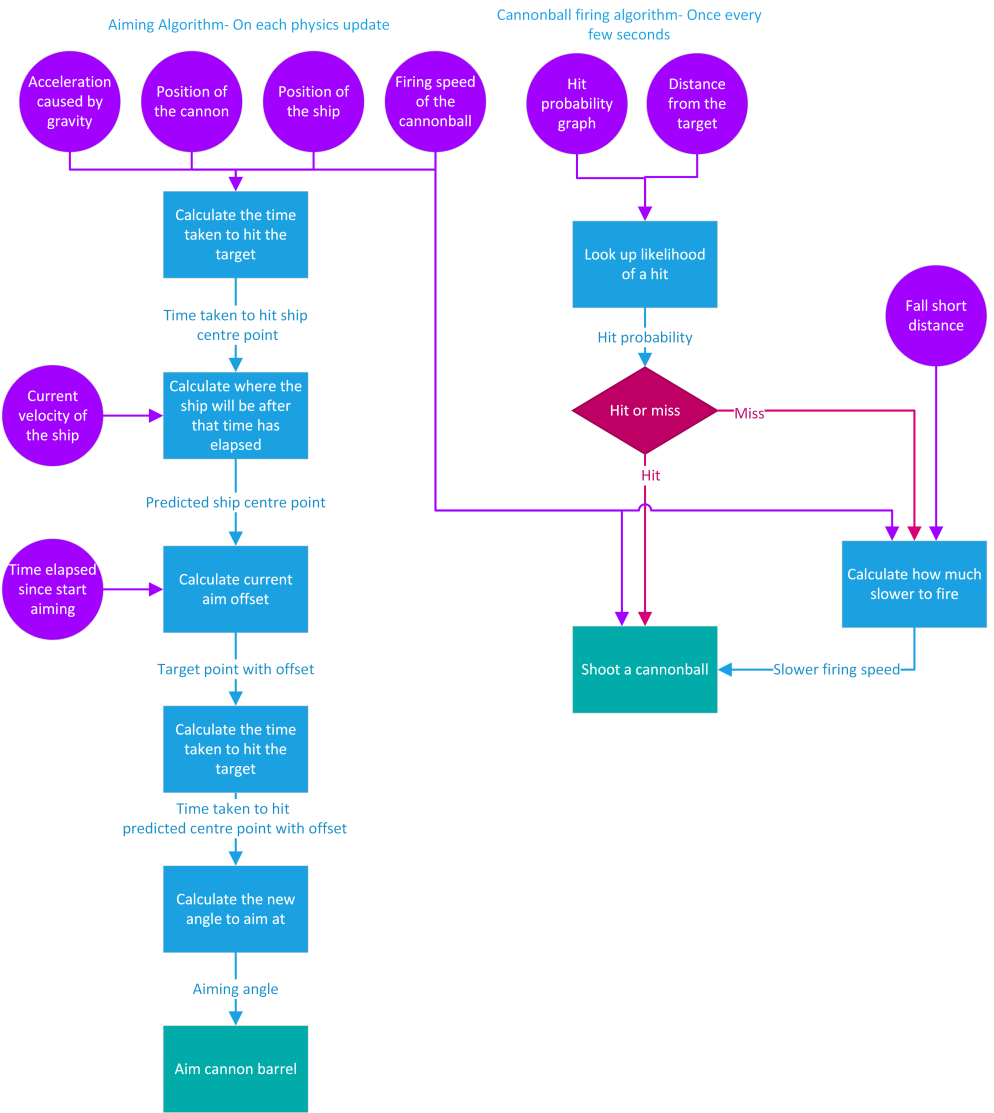
Now we have our skeletons reliably peppering ships with cannonballs, we can add the final layer of the algorithm – their ability to miss. We can decide before each shot in the cannon firing code whether it’ll be a hit or a miss by making a “dice roll”, set to the probability of a hit at this distance which we can read off a graph calibrated by a designer.
This is a really challenging problem to solve because even if we could tell the aiming code whether to aim to miss, it’d be a lot of work to get it to smoothly move the cannon barrel into position. Luckily there is one factor the cannon firing code has control over that affects the landing position of the cannonball – the speed of fire. Given that we’re aiming to always hit, if we decide an individual cannonball is supposed to miss we can fire it a little bit slower to make it land short.
If we want designers to be able to adjust how far short they want the cannonball to land, on each shot it can figure out how much slower it needs to shoot the “missed” cannonballs by using the SUVAT equations again.
A solid start
There are lots of ways to solve each problem in game development; another solution to this one could have been simply controlling the movement of the cannonball, instead of predicting where it will land based on the engine’s in-built physics. When making physics-based features like these, fakery can give you more control to design the experience, but real physics will work in a wider range of cases. For example, the recent addition of AI skeleton ships with skellies firing the cannons used this code as well, but it needed a little more adaptation to get it to work and look believable in the different scenario. The code looks very different now than it did a year ago, like most of the Sea of Thieves codebase. What this first algorithm did was give us the first few layers of detail that we could build on for more complex behaviour or new features.
As a big physics fan, this was one of my favourite features to work on. It’s also got a special place in my heart for the times I’ve been sent gameplay recordings of players getting hit directly in the face by a skelly cannonball, usually with a very irate caption! I do have to assure people regularly that the skellies can’t target particular players. It’s hard enough to predict where a ship will be by the time a cannonball lands, and a player can change direction a bit more sharply than a ship can! (I promise I didn’t just write this article to debunk that particular accusation)
I hope you can take away from this article what the anatomy of a gameplay feature can look like. Do understand that there are heaps of possible solutions here, this is just one that fits my skills and coding style, and the structure of the existing code, and gives the players the experience we wanted- that’s the joy of this kind of programming!
I’d like to make a big shout out to Shelley Preston who designed this feature and Andy Bastable and Rob Masella who also worked on programming it.
Thanks to my lovely colleagues for proof reading and giving their feedback:
- Rob Masella
- Jess Hider
- Topher Winward
- Chantelle Porritt
- Joe Neate
- James Thomas
- Shelley Preston
- Ted Timmins
(If I’ve forgotten you, come to my desk and make your best disappointed face)
What a great article, I loved learning about the mechanics of the cannon skellies.
LikeLiked by 1 person
A friend just sent me this. Really interesting reading and really well written. I’ve often wondered why Skeletons rarely shoot over the ship. So thank you!
I was wondering as I read – could you (if you haven’t already) change the initial aim (the bit where you calculate the initial time to hit) simply through a lookup table. That is, in a straight line, there’s only a finite number of positions a ship could be in from the skeleton. Say, 0 – 10ft, 10-20ft, etc. Have a lookup table with those time/distance pairs, and could maybe shave off a few cycles while maintaining fidelity. But it’s far from my job to teach you how to suck eggs, when you’ve done such great work so far.
Since I’m here, I’d like to ask if it would be possible/easy to add some sense of “visibility” to skeletons. I’m not asking as a demand that you change it – it’s more a thinking out loud, but I’d love to hear your ideas. So, at Shipwreck Bay (for example), it’s possible to dock behind the little arch and the skeleton on the cannon there will just pound cannonballs into the rocks, never hitting. Same at some forts, for that matter. How complicated would it be to have them calculate this, and try an up-and-over shot instead? Like, when they’re really close, but about to miss, they aim the cannon straight up. This sort of describes the difference a bit? https://www.desmos.com/calculator/4tkrgapau2
Whether you reply or not, thank you for an amazing game and I’m excited for the gamescom stuff coming up.
LikeLike
Good question, and the suggestion is good- But there’s a few reasons that the solution is as it is
– As it happens, while anything that does this much every tick is best cut down on, these kind of calculations aren’t very expensive- especially since there are unlikely to be more than a few active skelly cannons on the server at any one time. Loading up assets from disk can however be quite expensive!
– There’s quite a lot of variables involved in this, the table would have to include both the horizontal and vertical distance from the target, and the speed of the projectile
– Extensibility- We would have to keep the table up to date in case of any changes to the constants (projectile speed being the most likely candidates), which would probably mean having some step in the build process that generates it from the settings- a little more trouble than it’s worth
Given that they’re not too expensive it’s worth having the real maths because then we can plug it in for new features (Like the skeleton ships) and it’ll generally hold up
As for the visibility issue, off the top of my head, the “up and over” aiming could be quite a tricky fix. There are exactly two angles you could aim in to hit the same target without changing the projectile speed (which would require the shooting and aiming code to talk to each other). You might have noticed that this solution involves a quadratic so will output two possible flight times, corresponding to each aim config. However it’s possible to output a negative time (which indicates that the target is out of physical range), and the cannon’s aim movement is limited further in game, so this second aim angle isn’t always viable.
A better solution for the gameplay problem would probably just be making it stop shooting if the aim arc has something in it. Unfortunately this is probably on the list of things it would be lovely to fix but we’re always looking to maximise player impact for development time, so I can’t really say where that would fall on the priority list.
Thanks for your comment, and I’m glad you’re enjoying the game 🙂
LikeLike
Thank you so much for taking the time to reply!
LikeLike
I love how transparent the development team are. Actually taking the time to in depth explain how you’ve calculated each shot in a physics engine for no reason other than. To share the information with fans. I was part of the technical alpha and I’ve had a hard time trying to explain how much this has changed to my frie ds. Thanks for the article, it was as insightful as I could have hoped. Congrats rare for the crew you Assembled to make this game, from alpha to day 1 to becoming pirate legend this has been an experience I shan’t forget. PS. Please fire the guy who thought it was a good idea to give skellies snipers …or make them sit on the naughty step…or something…MAKE THEM PAY
LikeLike
sooo….Magic? 😀
LikeLike
Nope, just lots and lots of little bits of simple maths adding up to make something that looks like it!
LikeLike